Location: Home >> Detail
TOTAL VIEWS
Crop Breed Genet Genom. 2019;1:e190012. https://doi.org/10.20900/cbgg20190012
Department of Crop and Soil Sciences, Washington State University, Pullman, WA 99164, USA
* Correspondence: Dennis N. Lozada.
This article belongs to the Virtual Special Issue "Genetic Gains in Plant Breeding"
Incorporating secondary correlated traits collected from high-throughput phenotyping in genomic selection (GS) models for complex traits has been demonstrated to improve accuracy. The prediction ability of different single and multiple trait partial least square (PLS) regression models for grain yield were assessed for winter wheat lines evaluated in US Pacific Northwest environments. Different populations including a diversity panel, F5, and double haploid breeding lines were evaluated in Lind and Pullman, WA between 2015 and 2018 and were genotyped with genotyping by sequencing-derived SNP markers. Prediction ability was assessed under cross-validations and independent predictions. Multi-trait covariate models were advantageous in obtaining optimal predictions for yield, especially when there is less genetic relatedness between the training and test populations. Adding multiple traits in the model improved predictions for environments with low heritability. Cross-validations resulted in the highest prediction ability (0.16) whereas independent predictions using the diversity panel to predict F5 and double haploid winter wheat breeding lines obtained the lowest (0.002). Relatedness between populations, heritability of the secondary traits, and the type of PLS model used were among the principal factors affecting prediction ability. Our results showed the relevance of using multi-trait GS models to achieve increased predictions. Genetic architecture of the target trait and genetic relatedness between populations should be taken into consideration when choosing which type of models to implement in the breeding program. An increased prediction ability for the multi-trait models indicates the potential to attain improved genetic gains for yield in wheat breeding programs through these GS approaches.
The wealth of genomic information available for important crops has enabled the use of marker data for molecular breeding and DNA-based selection for plant improvement. In recent years, genomic approaches such as genome-wide association studies (GWAS) have been used to understand the genetic basis of important traits such as grain yield, disease resistance, and adaptation traits in wheat [1–4]. However, association mapping could not identify small effect loci and with such, the power of GWAS for the dissection of complex traits is limited [5,6]. In addition, the structure of breeding populations used in association mapping could cause the detection of spurious associations in genetic mapping [7]. On that regard, a complementary method, genomic selection (GS) has been explored in many crops and its potential to improve genetic gains though selection has been demonstrated [8–11].
In GS, a population with genotypic and phenotypic information is first used to train a prediction model (through a training population), and then used to predict the performance of lines in a validation set that have no phenotypic information [12]. The need to identify significant QTL-marker associations is removed, and instead GS considers numerous predictors simultaneously [13]. A measure of a model’s ability to perform trait predictions is its prediction ability, which could be defined as the correlation between observed phenotype with predicted values [14]. Through GS, genomic estimated breeding values (GEBV) can also be calculated and these values can be used for performing selections and choosing which parents to cross. Depending on the trait, a high or low estimated breeding value would indicate that a line is predicted to perform better in succeeding field trials. GS can increase genetic gains by reducing the number of cycles and progenies that need to be phenotyped and by improving the intensity of selection [15,16].
In addition to whole genome-wide marker data available for plant breeders, emerging tools for high-throughput phenotyping (HTP) have been widely utilized to collect phenotypic information in the field [17,18]. Its rapid development in the past few years resulted in increased amounts of phenotypic information available that could lead to better understanding of the complexity of traits such as grain yield [19,20]. Accurate phenotyping remains crucial for the efficient building of prediction models for GS [15]. Phenotyping platforms are typically equipped with different sensors such as red, green, and blue (RGB) cameras, multiple spectral cameras, and LiDAR, among others [21]. Ground-based HTP platforms with cameras that collect reflectance data from plant canopies have been used to assess various traits in different crops such as wheat [22–24], cotton [25], and rice [26]. Vegetation indices such as Normalized Difference Vegetation Index (NDVI), Normalized Water Index (NWI), and Simple Ratio (SR) derived from the absorbance of plant tissues at specific wavelengths of light are associated with important traits such as grain yield, biomass, plant water status, and degree of senescence [27–29]. HTP traits provide additional information on the genetic predictor variables in GS models and thus can be used to improve accuracies for complex traits such as grain yield [15]. Previously, incorporating these traits in genomic prediction models for grain yield resulted to improved predictions in wheat [30–32]. Combining information from HTP and genome-wide marker profile to identify lines with high genetic potential remain relevant for the improvement of grain yield especially in major wheat producing regions such as the Pacific Northwest area of the US.
Partial least square (PLS) regression takes advantage of correlated predictor variables X and response variables Y [33]. It relates both X and Y through a linear multivariate model and a dimension reduction approach which fits collinear genetic and environmental factors simultaneously by finding latent variables that explain the variance of the predictor variables as well as the covariance between predictor and response factors [34]. It is useful for predicting dependent variables from large number of predictors that might be highly correlated [35]. Moreover, PLS are computationally fast, statistically efficient, and can be used to address regression problems, predictions, classification, and survival analysis [36]. In Holstein bulls, PLS models were observed to be more accurate than pedigree based BLUP approaches in predicting traits with varying heritability [35]. Similarly, the robustness and superiority of these models over pedigree-based approaches for predicting milk yield, fat content, and somatic cell scores in dairy sheep has also been demonstrated [37]. PLS models have been used to predict grain yield [32]; yield, yield components and physiological traits [38]; and Septoria tritici blotch disease in wheat [39], among others. The feasibility of using these models for predicting yield in the presence of secondary traits in the model for Pacific Northwest winter wheat, nonetheless, has not been reported.
The objectives of this study were to compare single and multiple trait GS models for grain yield in US Pacific Northwest (PNW) winter wheat under different cross-validation and independent prediction scenarios, and to identify the prediction model resulting to optimal accuracies for yield. We evaluated the potential of using least square (PLS) regression models to predict grain yield for wheat in PNW growing conditions through using secondary traits collected from HTP field phenotyping.
The current study used five different populations of soft winter wheat adapted to the Pacific Northwest region of the US, including a diverse association mapping panel (DAP), F5, and double haploid (DH) populations described previously [40]. Briefly, DAP consisted of 456 lines evaluated in the Washington State University Dryland Research Station in Lind (LND) and in the Spillman Agronomy Farm near Pullman (PUL), WA during 2015–2018, whereas the F5 and DH populations were planted in LND and PUL in 2017 (F5_LND17 and F5_PUL17) and 2018 (DH_LND18 and DH_PUL18) growing seasons, respectively. F5_LND17 consisted of 61 whereas F5_PUL17 consisted of 501 lines. DH_LND18 and DH_PUL18 consisted of 449 and 761 winter wheat lines, respectively.
The winter wheat populations were planted in an augmented design [41] with repeated checks and genotypes (un-replicated) in each block. Plot length was 1.5 meter, each entry covered a 1 m2 area, planted at ~100 plants per m2. Checks used were “Eltan” [42] and “Madsen” [43] in LND; and Madsen was used in PUL for 2015−2018 seasons for the DAP. Lines “Bruehl” [44], Eltan, “Otto” [45], “Jasper” [46], Madsen, and “Xerpha” [47] were used as checks for F5_LND17; and “Brundage” [48], Jasper, Madsen, “Puma” [49], “UI Bruneau”, and “Xerpha” were used for the F5_PUL17 population. Checks used for the DH_LND18 lines included Jasper, Otto, and Xerpha; whereas Jasper, Madsen, Puma, and Xerpha were used as checks for the DH_PUL18 panel. The DAP was not evaluated for SRI and grain yield in LND in 2016 as substantial soil crusting caused delayed emergence for the winter wheat lines.
Collection and Analysis of Phenotypic DataGrain yield (in t·ha−1) was collected by harvesting whole plots using a Wintersteiger® Nursery combine (Ried im Innkreis, Austria). Spectral reflectance was collected using a CROPSCAN® multiple spectral radiometer (Rochester, MN, USA) attached to a pole and placed approximately 1 m above the canopy and in the middle of each plot. Filters measuring radiation at 16 different wavelengths of light (between 430 and 970 nm) were installed in the CROPSCAN. Data for spectral reflectance were taken approximately 10–15 days apart across three different growth stages- heading, early grain-fill and late grain-fill within a two-hour solar window (between 10:00 am and 2:00 pm) at clear and windless days. Spectral information for the plots were processed through the CROPSCAN MSR® software. Spectral reflectance indices, namely Normalized Difference Vegetative Index (NDVI), Normalized Water Index-1 (NWI-1), and Simple Ratio (SR) were calculated as shown in Table 1.
Adjusted means were calculated for an augmented design using the augmented complete block design (ACBD) in R program developed by Rodríguez et al. [53] for individual locations and combined across environments. Best linear unbiased estimates (BLUEs) and predictors (BLUPs) were calculated for individual locations and for combined analyses across environments, respectively. The models used for calculations were (a) Yij = µ + Blocki + IDCheck + Gen + Check + εij and (b) Yijkl = µ + IDCheck + Gen + Check + Loci + Loci × IDCheck + Loci × Gen + Loci × Check + Blockk(Loci) + εijkl, for individual environment, BLUE (a) and combined analyses across locations, BLUP (b), where Y is the trait of interest; µ is the effect of the mean; Blocki is the effect of the ith block; Gen corresponds to the un-replicated genotypes; Check is the effect of the replicated checks on each block; Loci is the effect of the ith location; IDCheck is the identifier of the checks; and ε is the standard normal errors [40]. Effects were considered fixed and random when calculating BLUEs for individual locations and BLUPs for combined analyses across environments, respectively.
Heritability and Genetic CorrelationsGenetic correlation (rG) was calculated according to Falconer [54] using the following formula: 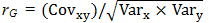 ; where Covxy is the covariance between yield and SRI calculated using a multivariate approach in JMP v. 8.1 [55]; and Varx and Vary are the variances for grain yield and SRI, respectively, across all locations for each population (DAP, DH, and F5 lines). Broad-sense heritability for grain yield in individual environments was calculated as
; where Covxy is the covariance between yield and SRI calculated using a multivariate approach in JMP v. 8.1 [55]; and Varx and Vary are the variances for grain yield and SRI, respectively, across all locations for each population (DAP, DH, and F5 lines). Broad-sense heritability for grain yield in individual environments was calculated as
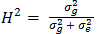 , where σ2g and σ2e are the genotype and error variance components, respectively;
, where σ2g and σ2e are the genotype and error variance components, respectively;
whereas H2 across locations (combined analyses) was calculated as 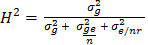 , where σ2g is the genotype variance; σ2ge is the variance due to genotype by environment interaction; n is the number of environments; r is the number of replication per environment (i.e., equal to 1 for an augmented design); and σ2e is the error variance using the augmented complete block design (ACBD) in R program [53].
, where σ2g is the genotype variance; σ2ge is the variance due to genotype by environment interaction; n is the number of environments; r is the number of replication per environment (i.e., equal to 1 for an augmented design); and σ2e is the error variance using the augmented complete block design (ACBD) in R program [53].
Genotyping was conducted using genotyping-by-sequencing [11] using the restriction enzymes MspI and PstI through the NC State Genomics Sciences Laboratory in Raleigh, NC, USA. After filtering for minor allele frequency MAF > 0.05 and quality control, 11,089 SNP markers, with 10,894 of these SNPs (98.2%) having known chromosome positions, were used for analyses. Imputation of missing data was done using the LDknni (linkage disequilibrium k-nearest neighbor joining imputation) function in TASSEL v. 5.0 [56]. Genetic relatedness between the training and validation populations was evaluated using Rogers genetic distance [57] through the “Population Measures” function in JMP v.8.1.
Genomic predictions were conducted using partial least square (PLS) regression with spectral reflectance data incorporated in the model following the methods of Crain et al. [32]. Prediction scenarios included cross-validations (CV) using a diversity association mapping panel (DAP); and two independent prediction (IP) schemes. In the CV, 80% of the lines was used to train a model to predict the remaining 20% under a five-fold validation. In the IP1 scenario, the DAP was used to predict grain yield of Washington State University F5 and DH winter wheat breeding lines; whereas in the second independent validation (IP2), predictions were conducted within the breeding lines. The BLUE and BLUP datasets for grain yield used for GS analyses are shown in Table 2. Mean spectral reflectance values across the three developmental stages were used as fixed effects in the PLS prediction models for yield.
The first PLS regression model used was a univariate model with the spectral reflectance measurements included as covariate predictor traits (Cov). The second model was a multivariate (MV) approach predicting yield together with the spectral reflectance traits. The basic form of the Cov model was: Grain yield = µ + Xβ + Zu + ε; where X is the matrix of individual observations (i.e., individual wheat lines); β is the fixed effects of spectral traits; Z is an (n × m) matrix assigning markers to genotypes; u is a (1 × n) array of random effects for the markers; and ε is the error [32]. Cov model, therefore, is a univariate model that includes predictor traits (in the form of spectral measurements) as covariates.
The MV model used was in the form:
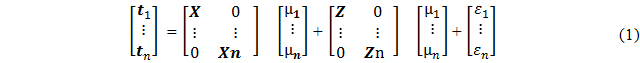
where n is the number of traits, t1 is a vector of trait values for grain yield; X is the matrix for fixed effects which simplifies to a vector of 1 for each trait representing the mean as only the markers were used in this model; Z is the random marker matrix for each trait; and ε1…n is the error term [32]. This model follows a scenario where grain yield is masked in the prediction model for the validation set, and therefore represents a breeding program where only spectral traits have been collected and the plants were not yet harvested, and hence lines are chosen primarily based on predicted values for grain yield [32]. Prediction ability was represented as the Pearson correlation coefficient between the predicted and actual grain yield values obtained by fitting HTP traits in the prediction model. Single trait prediction models included only a single spectral reflectance index, whereas multi-trait models included at least two spectral measurements for GS. All analyses were implemented under the partial least square (“pls”) package [58] in R. Additive and non-additive genetic variances for grain yield for each of the dataset were estimated using the “sommer” package through the “mmer” function [59] in R, using phenotypic and SNP marker data. The proportion of additive to the total genetic variance (i.e., additive + non-additive) was calculated by dividing the additive variance by the total genetic variance.
Broad-sense heritability for grain yield was low to moderate, ranging between 0.13 (F5_PUL17) and 0.70 (DAP_LND15). Yield had higher heritability in the DH lines (0.53 and 0.56 for DH_PUL18 and DH_LND18, respectively) compared with the F5 lines (0.13 (F5_PUL17) and 0.15 (F5_LND17)). In general, for the DAP, significant phenotypic correlations with grain yield were observed for the spectral traits (Table 3). Non-significant phenotypic correlations, nonetheless, were observed between SR and yield for DAP_LND18 and all the PUL datasets. Likewise, non-significant phenotypic correlations were observed for NDVI in PUL16 and PUL_Com, and PUL16, PUL18, and PUL_Com datasets for NWI-1. Significant phenotypic correlation between spectral traits and grain yield were observed for all the F5 and DH winter wheat breeding lines. Overall, higher H2 values were observed for the HTP traits. Heritability for the spectral traits ranged between 0.52 (NWI-1, DAP_LND18 and SR, F5_PUL17) and 0.95 (SR, DAP_LND17) dataset (Table 4). Genetic correlations using all locations for the different wheat populations ranged between −0.72 (NWI-1; DAP and F5 lines) and 0.78 (NDVI and SR, DAP) (Table 5). Genetic correlations between environments were low to moderate, ranging between −0.14 and 0.69 (DAP); −0.18 and 0.21 (DAP and the F5 and DH wheat breeding lines); and −0.13 and 0.30 (within the breeding lines) (Supplementary Tables S1–S3, respectively).
Analysis of principal components using genome-wide marker data revealed a 5.2% variation caused by the first PC (PC1) and 4.5% by PC2 within the F5 breeding lines, with no distinct clustering observed (Figure 1A). PC1 and PC2 caused 16.2 and 4.2% of variation, respectively within the DH lines (Figure 1B) with more differentiation observed compared with the F5, where the DH_LND lines formed a separate cluster with that of the DH_PUL lines. When combined on a single PCA biplot, the F5 lines formed a separate group from that of the DH lines, where the first PC caused 21.2% and the second PC caused 10.5% of variation. The DH entries formed separate clusters, indicating a higher genetic differentiation among them (Figure 1C). Genetic (Rogers) distances among the breeding lines were 0.05 (F5), 0.13 (DH) and 0.40 (F5 and DH).
 Figure 2. Boxplots of prediction ability for grain yield under different genomic selection scenarios using covariate (Cov) and multivariate (MV) partial least square regression models incorporating spectral reflectance traits. (A) cross validations using a diversity association mapping panel (DAP); (B) independent predictions using DAP to predict F5 and DH winter wheat breeding lines; and (C) independent predictions within the breeding lines. Actual values for prediction ability are reported in Supplementary Table S5. NDVI, Normalized Difference Vegetative Index; NWI-1, Normalized Water Index-1; SR, Simple Ratio.
Figure 2. Boxplots of prediction ability for grain yield under different genomic selection scenarios using covariate (Cov) and multivariate (MV) partial least square regression models incorporating spectral reflectance traits. (A) cross validations using a diversity association mapping panel (DAP); (B) independent predictions using DAP to predict F5 and DH winter wheat breeding lines; and (C) independent predictions within the breeding lines. Actual values for prediction ability are reported in Supplementary Table S5. NDVI, Normalized Difference Vegetative Index; NWI-1, Normalized Water Index-1; SR, Simple Ratio.
Boxplots showing prediction ability for the different GS schemes are shown in Figure 2A,C. Overall, prediction ability for yield ranged between −0.45 and 0.66. Prediction ability under a CV scenario using the DAP ranged between 0.02 and 0.27 (mean of 0.16) for single and multiple trait models. Using DAP to predict F5 and DH breeding lines (IP1) resulted to an average prediction ability of 0.06 and 0.07, respectively. Predictions within the breeding lines under independent validations (IP2) resulted to a mean prediction ability of 0.13, where predicting within the same population resulted in a 36% increase in average prediction ability compared with using the F5 to predict the DH lines (and vice versa). Prediction ability using covariate models was significantly higher (P < 0.05) than the predictions for multivariate models under single and multiple traits and across all prediction scenarios (Figure 3). Similarly, significant (P < 0.05) differences were observed for the mean prediction ability using multiple traits compared with using only a single trait in the model (0.15 vs 0.09) across all GS scenarios. Predicting within similar environments resulted in a 13% advantage compared to across environment predictions. Overall, a positive correlation (r = 0.35) between the proportion of additive variance to the total genetic variance and mean prediction ability across datasets was observed (Supplementary Table S4).
 Figure 3. Mean prediction ability across all genomic selection scenarios for grain yield using partial least square covariate (Cov) and multivariate (MV) regression models in the presence of single (ST) and multiple (MT) traits collected from high-throughput phenotyping. Prediction scenarios included cross-validations and independent predictions. Means followed by the same letter are not significantly different, LSD < 0.05.
Figure 3. Mean prediction ability across all genomic selection scenarios for grain yield using partial least square covariate (Cov) and multivariate (MV) regression models in the presence of single (ST) and multiple (MT) traits collected from high-throughput phenotyping. Prediction scenarios included cross-validations and independent predictions. Means followed by the same letter are not significantly different, LSD < 0.05.
The current study reports the prediction ability of single and multiple trait GS models for grain yield incorporating spectral reflectance measurements derived from high-throughput field phenotyping. Different prediction scenarios for empirical datasets in a winter wheat breeding program were evaluated for the prediction ability of grain yield. Prediction ability of covariate and multivariate PLS regression models for yield were compared across different datasets and prediction scenarios in winter wheat grown in the PNW region of the US.
Prediction Ability for Single and Multiple Trait Genomic Selection ModelsPrevious studies have shown the relevance of using secondary traits to predict a focal trait, which is often difficult to phenotype or measure (e.g., grain yield). In US Holsteins, GS accuracy improved when switching from single- to multi-trait models across different traits [60]. Similarly, in African cassava, multi-trait and multi-environment mixed models were recommended for selection, as using these models resulted in a 40% improvement in prediction ability of target agronomic traits [61]. The advantage of multi-trait models over the single trait relies mainly on the use of genetically correlated traits for predictions [62]. Thus, genetic correlation between the primary and the predictor traits is crucial to achieve optimal GS accuracies in the breeding program. In the present work, the genetic correlations between the measured SRI across locations and grain yield were high, indicating their potential to be used as secondary traits to achieve increased prediction ability for yield in US PNW winter wheat.
Multi-trait prediction models showed a 40% advantage over the single-trait model across GS scenarios in the current study. Increasing the number of traits in the model was relevant in increasing prediction ability, where using all three traits resulted to the highest mean and was significantly different (P < 0.05) with the predictions using a single-trait model. In some scenarios, however, having three indices in the model did not necessarily result to higher predictions compared to the two-trait models. It was previously observed that including more traits did not show advantage in predicting yield and protein content in rye, as additional traits could introduce issues in co-linearity [63]. Furthermore, it was noted that if the aim of a breeding program is to improve the prediction ability, particularly for a scarcely phenotyped trait, using a two-trait instead of a three-trait model could offer a greater advantage [63]. In this context, it would thus be beneficial to identify only a few of the highly heritable, strongly correlated predictor traits and use these routinely for indirect selection and prediction of the target or primary trait. In our case, using NDVI and SR in combination under a covariate model as fixed effect predictor traits showed the highest average prediction ability across all scenarios (0.15), and therefore could be used to improve predictions for grain yield in US PNW winter wheat.
Other studies observed that using multiple traits in the prediction model did not result in improved predictions [64,65] demonstrating that in some cases, multi-trait models are not advantageous compared to single trait approaches. Overall, although we observed generally low values for the prediction ability of grain yield in the current study, integrating GS strategies in the breeding program should still be considered. In the long run, the gains achieved using these approaches through increased selection intensity and faster breeding cycles should give additional advantage over the traditional marker or phenotypic selection [15,16]. Furthermore, prediction ability could be improved by optimizing different factors that affect GS accuracy such as the genetic architecture of the trait, heritability, number of markers, genetic and phenotypic correlations among the traits, and the percentage of missing data, either alone or in combination [66–68]. Ultimately, the success of genomic predictions in breeding programs does not all depend on the calculated prediction ability [69] but on how breeders will use this information in performing guided decisions on which lines to advance or used as parents. There were no significant differences between predictions when single and multiple traits were used in CV and IP1 scenarios. Nevertheless, when predictions were conducted within the breeding lines (IP2), where genetic relatedness is more apparent than in IP1, using multiple traits resulted in a significant (P < 0.05) increase in prediction ability for grain yield, where a 67% advantage over using only a single trait in the GS model was observed. When there is less relatedness between the training and test populations, the use of multi-trait models should be preferred over single trait approaches [70].
Prediction Ability across Different GS ScenariosCross-validations (CV) represent a common prediction scenario where a single population is divided into a training and a testing set, whereas in independent predictions, a model is trained in one population and is later used to predict another comprising of untested genotypes in untested environments [71]. Overall, using CV resulted to the highest average predictions (0.16) followed by IP2 (0.13) and IP1 (0.01), similar with previous results comparing accuracy for CV and independent validations in DH wheat [72]. The increased prediction ability in the CV scenario could be the result of using the same environmental conditions in which both the training and validation populations are evaluated [73]. Nonetheless, independent validations present a more realistic approach to plant breeding, as this GS strategy aims to predict the performance of lines that are yet to be evaluated in different environments or trials. In CV, we observed significant differences in prediction ability between using combined (BLUP) and individual (BLUE) datasets for predictions (0.19 vs 0.12), showing the advantage of combining environments across different years to capture variability for grain yield. Moreover, predicting within the same environment (e.g., LND predicting LND) for the IP1 scenario was significantly higher compared to across environment predictions (P < 0.0001), demonstrating the relevance of predicting within the same environment as effects of QTLs could vary across different environments and lead to poor prediction accuracies [74]. The variability of prediction ability values observed across different scenarios and datasets could be primarily due to the differences across the environments used for predictions, as indicated by low to moderate genetic correlations among the environments (Supplementary Tables S1–S3). The proportion of additive variance to the total genetic variance across different datasets was also related to improved prediction ability. In general, it was observed that the higher the proportion of additive variance, the higher the mean prediction ability across datasets. A positive correlation (r = 0.35) between prediction ability and additive variance to total genetic variance ratios was observed across the datasets used for analyses.
Prediction Ability for Covariate and Multivariate ModelsCovariate models incorporating reflectance indices as fixed effect predictor traits resulted in higher accuracies compared to multivariate across all prediction scenarios (0.10 vs 0.02). Using covariate multi-trait models further resulted in a 50% gain in prediction ability compared to using covariate single-trait model, whereas no significant differences were observed within multivariate models regardless of the number of secondary traits. In contrast with our results, the superiority of multivariate models for predicting yield has been previously demonstrated in wheat [32,75]. Our results thus rendered some interesting observations regarding the use of these types of models for predicting grain yield in the presence of secondary traits across different CV and IP scenarios for PNW winter wheat.
First, multivariate models might not be advantageous for predicting lines with little or no genetic relatedness even when there is a high genetic correlation between the predictor and target traits, as in our case. Similar with the IP1 scenario, when a breeding panel was previously used to predict wheat DH lines, reduced predictions were observed in wheat, which was attributed to the presence of opposite linkage phases between SNPs and QTL for yield for genetically distant populations [76]. We observed the relevance of relatedness between the training and validation panels to achieve maximum prediction ability, particularly under the IP2 scenario, consistent with previous studies which highlighted the importance of genetic relationships between the populations used for predictions [77–80]. Among the breeding lines, an increased genetic (Rogers) distance between the training and test panels was related to a decrease in accuracy. Altogether, highest mean prediction ability was observed for the F5 lines (0.16), followed by the DH (0.14), and the across population predictions (0.11), with Rogers distance of 0.05, 0.13, and 0.40, respectively. PCA revealed less genetic differentiation among the F5 lines, whereas the DH lines formed two distinct clusters, based on location. Predicting within the populations (i.e., F5 predicting F5; DH predicting DH lines) showed a 36% advantage compared to across population predictions, indicating the need to use genetically related populations to achieve optimal prediction ability.
Second, incorporating multiple traits is essential to achieve optimal predictions when the target trait has low heritability. A 43% and 64% increase in prediction ability was observed for multi-trait models for the low heritability datasets LND17_F5 (H2 = 0.15) and PUL17_F5 (H2 = 0.13). Likewise, Guo et al. [81] previously observed that multi-trait approaches performed better than single trait models when evaluating traits with low heritability and lots of missing data using simulations. Furthermore, multi-trait analysis enabled more accurate predictions of breeding values for low heritable traits (heritability of 0.10) that are correlated with highly heritable traits (heritability of 0.80) by utilizing correlation structure between traits under a Bayesian regression model [82]. In barley, PLS did not perform well on traits with medium or high heritability and a smaller training set [83]. Overall, although the observed heritability values for grain yield in the current study were within the range of published values in wheat [4,84,85], we still observed a weak correlation (r = 0.06) between heritability and mean prediction ability across datasets for the cross-validations. There was also no significant difference in average accuracies in using the DH datasets (where grain yield had higher heritability values) for predictions in the IP2 scenario. Taken together, these observations suggest that the heritability of the target trait was secondary only to genetic relatedness and the type of prediction model affecting GS accuracy for yield in PNW winter wheat. It was interesting to note, nevertheless, that the heritability of the secondary spectral traits was related to improved predictions in the covariate PLS models, where using SR (H2 between 0.52 and 0.95) for GS significantly improved prediction ability for yield (Figure 2C) under the IP2 scenario. This suggests that the prediction ability of a lowly heritable target trait could be improved by using one or multiple secondary predictor traits with higher heritability when using genetically related populations under covariate models. Lastly, size of the training population was relevant to attain improved accuracies, particularly in the IP2 scenario where predictions where done within the breeding lines (with differing size of the TP), consistent with previous studies demonstrating the importance of TP size in achieving optimal accuracy [67,80,86,87]. Using larger population sizes as TP (PUL17 and PUL18) resulted to an average of 14% increase in the prediction ability for yield in the IP2 scenario.
The multivariate approach implemented in the current study resembles a breeding program where plots are yet to be harvested, similar with earlier methods used in wheat [32,75]. This scenario then allows breeders to select for yield based on the predicted values from GS models that incorporate secondary spectral reflectance traits. Previously, it has been shown that these secondary spectral traits have a huge potential for the indirect selection of yield in US Pacific Northwest winter wheat, since they have high genetic and phenotypic correlations [24,40]. Additionally, it has been shown that the inclusion of these traits in prediction models could improve the accuracy for yield [30,32,75]. Breeders could therefore use these HTP traits, which could be collected in either single plants or in plots, as proxy measurements for yield potential, as a basis of selecting higher yielding lines throughout the growing season as they could be predictive of the final yield observed in the field.
The prediction ability of single and multiple trait prediction models for yield in PNW winter wheat was evaluated. Our results showed the feasibility of using least square regression models incorporating secondary traits to predict yield in soft winter wheat. Covariate models were superior to multivariate in predicting grain yield in the presence of secondary traits from high-throughput field phenotyping. Multi-trait models also showed an advantage over single trait prediction models for grain yield. The influence of relatedness and size of the training population on genomic selection accuracy was observed, whereas there was no apparent relationship between heritability and prediction ability. When using related populations, using of highly heritable HTP traits such as simple ratio, either alone or in combination with other spectral traits significantly improved prediction ability for yield under the covariate models. Predicting within the same environments resulted to higher accuracies. Overall, the results presented herein demonstrated the power of combining different genomic and phenotypic approaches to accelerate plant breeding and the potential to improve genetic gains for complex traits in wheat breeding programs. Other prediction models such as multivariate Bayesian, genomic BLUP, and machine learning approaches will also be explored for these GS scenarios for grain yield in the WSU winter wheat breeding program.
The dataset of this study is available from the authors upon reasonable request.
DNL performed genomic prediction analyses and wrote a draft of the manuscript; AHC edited the manuscript and obtained funding for the project.
The authors declare no conflict of interest.
The study was funded the National Institute of Food and Agriculture (NIFA) of the U.S. Department of Agriculture (Award number 2016-68004-24770) and Hatch project 1014919.
The authors would like to thank Dr. Jared Crain (Kansas State University, Manhattan, KS, USA) for assistance in the genomic selection analyses; and Dr. Jayfred Godoy, Gary Shelton, Kyall Hagemeyer, and Jason Wigen for collection of phenotypic data.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
Lozada DN, Carter AH. Accuracy of Single and Multi-Trait Genomic Prediction Models for Grain Yield in US Pacific Northwest Winter Wheat. Crop Breed Genet Genom. 2019;1:e190012. https://doi.org/10.20900/cbgg20190012

Copyright © 2020 Hapres Co., Ltd. Privacy Policy | Terms and Conditions